Investigacion proyeccion en perspectiva. ortogonal y puerto de vision y ventanas

Investigar:
concepto y como manejar estos conceptos en Opengl
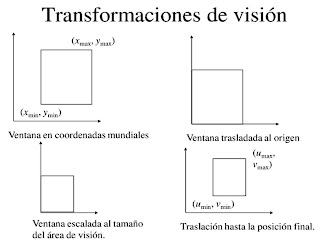
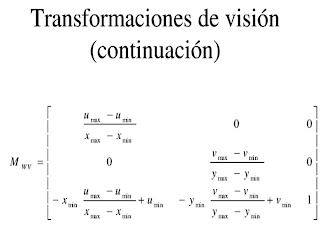
puerto de vision y ventanas
Poyeccion ortogonal
proyeccion en perspectiva

 

En geometría euclidiana, Proyección ortogonal es aquella cuyas rectas proyectantes auxiliares son perpendiculares al plano de proyección (o a la recta de proyección), estableciéndose una relación entre todos los puntos del elemento proyectante con los proyectados.
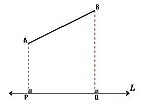
En el plano, la proyección ortogonal es aquella cuyas líneas proyectantes auxiliares son perpendiculares a la recta de proyección L.
Así, dado un segmento AB, bastará proyectar los puntos "extremos" del segmento –mediante líneas proyectantes auxiliares perpendiculares a L–, para determinar la proyección sobre la recta L.
Una aplicación de proyecciones ortogonales son los teoremas de las relaciones métricas en el triángulo mediante las cuales se puede calcular la dimensión de los lados de un triángulo.
El concepto de proyección ortogonal se generaliza a espacios euclidianos de dimensión arbitraria, inclusive de dimensión infinita. Esta generalización juega un papel importante en muchas ramas de matemática y física.

Casos de proyección ortogonal en el plano

Proyección ortogonal de un punto

• La proyección ortogonal de un punto P en una recta L es otro punto A que se obtiene trazando una línea auxiliar perpendicular a L desde el punto A tal que esta línea pase por P. Lógicamente, si el punto P pertenece a la recta L, coinciden: P = A .

Proyección ortogonal de un segmento

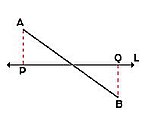
• Caso general: si el segmento dado AB no es paralelo a la recta L, la proyección ortogonal es un segmento PQ que se obtiene trazando líneas perpendiculares a L desde los puntos extremos de AB. La magnitud de la proyección siempre es menor que la del segmento dado.

• Si el segmento PQ y la recta L son paralelos, la proyección será: AB = PQ, que se obtiene de forma análoga.

• Si el segmento AB tiene un punto común con la recta L, la proyección se obtiene de modo similar.

• Si el segmento AB corta a la recta L, la proyección se obtiene de forma análoga.

PROYECCION EN PERSPECTIVA

La Infografia 3d o perpectivas 3d, es una técnica de creación de imágenes virtuales tridimensionales mediante avanzadas técnicas informáticas.

Infografia y Arquitectura 3d.

La infografia aplicada al mundo de la arquitectura (infoarquitectura), es una herramienta que está adquiriendo gran protagonismo en estudios de arquitectura e interiorismo, constructoras, ingenierías e inmobiliarias, gracias a las posibilidades que esta tecnología ofrece para la proyección, presentación y promoción de proyectos arquitectónicos y urbanísticos.

Principales ventajas que nos ofrece las infografías 3d:
-Facilita la comprensión del proyecto arquitectonico por parte del cliente (en especial cuando se trata de venta sobre plano de viviendas).
-Permite comprobar el resultado final de la obra sin construirla, y estudiar su volumetría, los materiales, el color, la luz, etc.
- Permite valorar el impacto visual de la construcción en el entorno.
-Permite la presentación de una idea a concurso, dotando a su proyecto y a la empresa de una imagen potente.

Las perspectivas de arquitectura en 3D son, sin duda, la mejor forma de mostrar con todo lujo de detalle lo que simplemente está proyectado. A un solo paso de una imagen real con la arquitectura multimedia 3D, para mostrar con la mayor fidelidad posible cuál será el resultado final. Integración completa del 3D en imágenes reales para conseguir un acabado impecable.

El diseño de interiores con infografía 3D es una inestimable ayuda para llegar a visualizar con toda exactitud la magnitud del espacio, la disposición de los muebles, las posibilidades de decoración… para ver el calor de un hogar en lugar de sólo líneas.
Otros nombres como se les conoce es Maquetas Virtuales,Renders,Perspectivas 3D fotorealistas, perspectivas arquitectonicas.

Read more: http://www.arquigrafico.com/las-perspectivas-o-infogafias-3d-en-la-arquitectura#ixzz2QjqnmiVt