Este tipo de curvas fue desarrollado por Pierre Bézier por encargo de la empresa de automóviles Renault™ que buscaba una representación matemática para definir las transiciones suaves en la curvatura de las líneas de sus automóviles.

Se generan a partir de funciones polinómicas de grado tres que permiten la representación de cualquier forma curvada y evitan la complicación innecesaria de cálculos matemáticos que se produciría usando polinomios de mayor grado.
Cualquier trazado de estas características está definido por una serie de puntos por los que pasa la curva y otros exteriores a ella que definen sus puntos de inflexión, es decir, aquellos en que cambia de curvatura, pasando de cóncava a convexa o viceversa.

Manejadores de la curva
En un trazado Bézier existen "manejadores" en cada uno de sus nodos de manera que se puede alterar la curvatura a voluntad para adaptar el trazo a cualquier forma imaginable, controlando la suavidad de las zonas de transición.
La forma paramétrica de la curva es:
En el subcampo de la informática de diseño asistido por computadora y de gráficos por computadora, el término B-spline se refiere con frecuencia a una curva parametrizada por otras funciones spline, que se expresan como combinaciones lineales de B-splines (en el sentido matemático anterior). Una B-spline es simplemente una generalización de una curva de Bézier, que puede evitar el fenómeno Runge sin necesidad de aumentar el grado de la B-spline.
Definición
Dado m valores reales ti, llamados nudos, con
![\mathbf{S}(t)= \sum_{i=0}^{m-n-2} \mathbf{P}_{i} b_{i,n}(t) \mbox{ , } t \in [t_{n-1},t_{m-n}]](//upload.wikimedia.org/math/e/d/5/ed56946ccf2a0463661b36606cecb760.png) .
.
Las m-(n+1) B-splines básicas de grado n se pueden definir mediante la fórmula de recursión Cox-de Boor
Nótese que j+n+1 no puede exceder de m-1, lo que limita tanto a j como a n.
B-spline uniforme
Cuando la B-spline es uniforme, las B-splines básicas para un determinado grado n son sólo copias cambiadas de una a otra. Una alternativa no recursiva de la definición de la B-splines m-n+1 básica esB-spline cardinal
Si se define B0 como la función característica de![[-\tfrac{1}{2}, \tfrac{1}{2}]](http://upload.wikimedia.org/math/1/9/a/19a2ea4a10660560d6779686604a0c8d.png) , y Bk recursivamente como el producto convolución
, y Bk recursivamente como el producto convoluciónBk tiene soporte compacto
![[-\tfrac{k+1}{2}, \tfrac{k+1}{2}]](http://upload.wikimedia.org/math/4/9/f/49f088871626685ab979ba1845c5a7ee.png) y es una función impar. Como
y es una función impar. Como 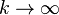 las B-splines cardinales normalizadas tienden a la función de Gauss.[5]
las B-splines cardinales normalizadas tienden a la función de Gauss.[5]Notas
Cuando el número de puntos de control de Boor es el mismo que el grado, la B-Spline degenera en una curva de Bézier. La forma de las funciones base es determinada por la posición de los nudos. Escalar o trasladar el vector de nudo no altera las funciones de base.El spline está contenido en el casco convexo de sus puntos de control. Una B-spline básica de grado n
La función base se pueda obtener del polinomio de Bernstein.
Ejemplos
A continuación se muestran una serie de ejemplos de diversos tipos de B-splines.B-spline constante
La B-spline constante es la spline más simple. Se define en un solo tramo de nudo y ni siquiera es continua en los nudos. Es sólo la función indicador de los diferentes tramos de nudo.B-spline lineal
La B-spline lineal se define en dos tramos de nudo consecutivos y es continua sobre los nudos, pero no diferenciable.B-spline cuadrática uniforme
Las B-splines cuadráticas con nudo-vector uniforme es una forma común de B-spline. La función base puede ser calculada fácilmente , y es igual para cada segmento, en este caso.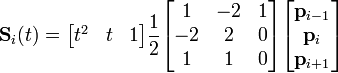 para
para ![t \in [0,1], i = 1,2 \ldots m-1](//upload.wikimedia.org/math/c/5/2/c525eb4e77ed286a7e4145114dc40cc2.png)
B-spline cúbica
Una formulación B-spline para un solo segmento puede ser escrita como: donde el
donde el  es el peso, tirando de la curva hacia el punto de control
es el peso, tirando de la curva hacia el punto de control  mientras que aumenta o se desplazan fuera de la curva, a la vez que disminuye.
mientras que aumenta o se desplazan fuera de la curva, a la vez que disminuye.Toda una serie de segmentos, las curvas m-2 (
 ) definidas por m+1 puntos de control (
) definidas por m+1 puntos de control (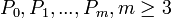 ) como un B-spline en t, se definiría como:
) como un B-spline en t, se definiría como:Hay dos tipos de B-spline - uniforme y no uniforme. Una B-spline no uniforme es una curva donde los intervalos entre los puntos sucesivos de control no son, o no necesariamente son, iguales (el vector de nudos de espacios de nudo interiores no son iguales). Una forma común es donde los intervalos se reducen sucesivamente a cero, interpolando los puntos de control.
B-spline cúbica uniforme
La B-spline cúbica con vector-nudo uniforme es la forma más usual de B-spline. La función base puede ser fácilmente calculada, y es igual para cada segmento, en este caso. Puesto en forma de matriz, esto es: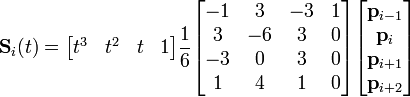 para
para ![t \in [0,1].](//upload.wikimedia.org/math/d/e/4/de4ef1e33d30a0fa6fc661f8fed20bde.png)
Especificaciones técnicas
Una curva NURBS se define por su grado, un conjunto de puntos de control ponderados, y un vector de nodos. Las curvas y superficies NURBS son generalizaciones de curvas B-splines y curvas de Bézier, así como de superficies, siendo su diferencia principal la ponderación de los puntos de control que hacen a las curvas NURBS racionales (las curvas B-splines racionales no uniformes son un caso especial de las curvas B-splines racionales). Mientras que las curvas de Bézier se desarrollan en una sola dirección paramétrica, normalmente llamada s o u, las superficies NURBS evolucionan en dos direcciones paramétricas, llamada s y t o u y v.
Mediante la evaluación de una curva de Bézier o una curva NURBS en diversos valores del parámetro, la curva se puede representar en un espacio Cartesiano de dos o tres dimensiones. Asimismo, mediante la evaluación de una superficie NURBS en diversos valores de los dos parámetros, la superficie se puede representar en el espacio cartesiano.
Las curvas y superficies NURBS son útiles por varias razones:
- Son invariantes bajo transformaciones afines,así como de perspectiva: operaciones de rotación y traslación se pueden emplear en las curvas y superficies NURBS aplicándolas a sus puntos de control.
- Ofrecen una estructura matemática común para figuras analíticas estándar (por ejemplo, cónicas) y figuras de forma libre.
- Proporcionan flexibilidad para diseñar una gran variedad de figuras.
- Reducen el consumo de memoria al almacenar figuras (en comparación con métodos más sencillos).
- Pueden ser evaluados rápidamente por algoritmos numéricamente estables y precisos.
Puntos de control
Los puntos de control determinan la forma de la curva. Generalmente, cada punto de la curva se calcula tomando la suma ponderada de una serie de puntos de control. El peso de cada punto varía de acuerdo con el parámetro que lo rige. Para obtener una curva de grado d, el peso de cualquier punto de control es diferente de cero sólo en D +1 intervalos del espacio de parámetros. Dentro de estos intervalos, el peso cambia de acuerdo a una función polinómica (funciones de base) de grado d. En los límites de los intervalos, las funciones base se aproximan lentamente a cero, determinando esta velocidad con el grado del polinomio. Como ejemplo, la función base de grado uno es una función triangular. Incrementa desde cero a uno, después decrementa de nuevo a cero. Mientras se incrementa, la función base del punto de control anterior cae. De esta manera, la interpolación entre los dos puntos es una curva, y esta curva resultante es un polígono, que es [[Función_continua|continua], pero no diferenciable en los límites del intervalo, o los nodos. Polinomios de grado superior, en consecuencia, tienen más derivadas continuas. Se debe tener en cuenta que dentro del intervalo la naturaleza polinómica de las funciones base y la linealidad de la construcción hace a la curva perfectamente suave, por lo que es sólo en los nodos que puede surgir discontinuidad.El hecho de que un único punto de control sólo influye en aquellos intervalos en los que es activa es una propiedad muy deseable, es conocido como apoyo local. En el modelado, esto permite el cambio de parte de una superficie, mientras las otras partes se mantienen igual.
Agregar más puntos de control permite una mejor aproximación a una curva dada, aunque sólo cierta clase de curvas se puede representar exactamente con un número finito de puntos de control. Las curvas NURBS también cuentan con un peso escalar para cada punto de control. Esto permite mayor control sobre la forma de la curva sin aumentar indebidamente el número de puntos de control. En particular, se añaden secciones cónicas como círculos y elipses al conjunto de curvas que se pueden representar exactamente. El término racional en NURBS se refiere a estos pesos.
Los puntos de control pueden tener cualquier dimensión. Los puntos de una dimensión sólo definen una función escalar del parámetro. Estos se utilizan normalmente en los programas de procesamiento de imagen para ajustar el brillo y las curvas de color. Los puntos de control tridimensionales se utilizan mucho en el modelado 3D, donde se emplean cotidianamente como referencia de la palabra "punto", un lugar en el espacio 3D. Los puntos multidimensionales pueden ser usados para controlar conjuntos de valores en base al tiempo, por ejemplo, los diferentes ajustes de posición y de rotación del brazo de un robot. Las superficies NURBS son sólo una aplicación de esta. Cada "punto" de control es en realidad un vector lleno de puntos de control, definiendo una curva. Estas curvas comparten su grado y el número de puntos de control, y abarcan una dimensión del espacio de parámetros. Por interpolación de estos vectores de control sobre la otra dimensión del espacio de parámetros, un conjunto continuo de curvas es obtenido, definiendo la superficie.
Vector de nodos
El vector de nodos es una secuencia de valores de parámetros que determinan dónde y cómo los puntos de control afectar a la curva NURBS. El número de nodos es siempre igual al número de puntos de control más el grado de la curva menos uno. El vector de nodos divide el espacio paramétrico en los intervalos mencionados antes, normalmente conocidos como segmentos de nodo. Cada vez que el valor del parámetro introduce un nuevo segmento de nodo, un nuevo punto de control se activa, mientras que un punto de control antiguo se descarta. De ello se deduce que los valores en el vector de nodos deben estar en orden ascendente, por lo que (0, 0, 1, 2, 3, 3) es válido, mientras que (0, 0, 2, 1, 3, 3) no lo es.Nodos consecutivos pueden tener el mismo valor. Esto define entonces un segmento de nodo de longitud cero, lo que implica que dos puntos de control se activan al mismo tiempo (y, por supuesto, dos puntos de control antiguos se desactivarán). Esto tiene un impacto en la continuidad de la curva resultante o de sus derivadas más altas, por ejemplo, permite la creación de esquinas en una curva NURBS suavizada. Un número de nodos que coinciden se denomina a veces como un nodo con cierta multiplicidad. Nodos con multiplicidad dos o tres se conocen como nodos dobles o triples. La multiplicidad de un nodo se limita al grado de la curva, puesto que una multiplicidad mayor dividiría a la curva en partes inconexas y dejaría a los puntos de control sin usar. Para NURBS de primer grado, cada nodo se asocia a un punto de control.
El vector de nodos por lo general comienza con un nodo que tiene una multiplicidad igual a la orden. Esto tiene sentido, ya que activa los puntos de control que influyen en el primer segmento de nodo. Del mismo modo, el vector de nodos por lo general termina con un nodo de esa multiplicidad. Curvas con tales vectores de nodos inician y terminan en un punto de control.
Los valores individuales de los nodos no son significativos por sí mismos, sólo importa la proporción de diferencia entre los valores de los nodos. Por lo tanto, los vectores de nodos (0, 0, 1, 2, 3, 3) y (0, 0, 2, 4, 6, 6) producen la misma curva. Los valores de las posiciones de los nodos influyen en el mapeo del espacio de parámetros al espacio de la curva. La renderización de una curva NURBS se hace generalmente en pasos con distancia fija a través del rango de parámetros. Mediante el cambio de las longitudes de los segmentos de nodo, se pueden utilizar más puntos de muestra en regiones donde la curvatura es máxima. Otro uso es en situaciones en las que el valor del parámetro tiene algún significado físico, por ejemplo, si el parámetro es el tiempo y la curva describe el movimiento del brazo de un robot. Las longitudes del segmento de nodo luego se traducen en velocidad y aceleración, que son esenciales para evitar daños al brazo robótico o su entorno. Esta flexibilidad en el mapeo es a lo que la frase no uniforme en NURBS se refiere.
Necesarios sólo para los cálculos internos, los nodos generalmente no son útiles para los usuarios de modelado de software. Por lo tanto, muchas aplicaciones de modelado no hacen a los nodos editables o incluso visibles. Por lo general es posible establecer vectores de nodos razonables observando la variación en los puntos de control. Las versiones más recientes de software para NURBS (por ejemplo, Autodesk Maya y Rhinoceros 3D) permiten la edición interactiva de las posiciones de los nodos, pero esto es significativamente menos intuitivo que la edición de puntos de control.
Grado
El orden de una curva NURBS define el número de puntos de control cercanos que influyen en cualquier punto en la curva. La curva es representada matemáticamente por un polinomio de grado uno menos el orden de la curva. Por lo tanto, las curvas de segundo orden (que están representadas por polinomios lineales) se denominan curvas lineales, las curvas de tercer orden, se denominan curvas cuadráticas, y las curvas de cuarto orden se denominan curvas cúbicas. El número de puntos de control debe ser mayor que o igual al orden de la curva.En la práctica, las curvas cúbicas son las más utilizadas. Las curvas de quinto y sexto orden a veces son útiles, sobre todo para la obtención de derivadas continuas de orden mayor, pero las curvas de órdenes más altos prácticamente nunca se utiliza porque conducen a problemas numéricos internos y tienden a requerir tiempos de cálculo desproporcionadamente grandes.
![\mathbf{B}(t)=\mathbf{P}_0 + (\mathbf{P}_1-\mathbf{P}_0)t=(1-t)\mathbf{P}_0 + t\mathbf{P}_1 \mbox{ , } t \in [0,1].](http://upload.wikimedia.org/math/5/3/f/53f70cb65e4c07b3cc58d1d5ba76b72c.png)
![\mathbf{B}(t) = (1 - t)^{2}\mathbf{P}_0 + 2t(1 - t)\mathbf{P}_1 + t^{2}\mathbf{P}_2 \mbox{ , } t \in [0,1].](http://upload.wikimedia.org/math/b/0/a/b0a53071f8baba155c699a30f26f60b0.png)
![\mathbf{B}(t)=\mathbf{P}_0(1-t)^3+3\mathbf{P}_1t(1-t)^2+3\mathbf{P}_2t^2(1-t)+\mathbf{P}_3t^3 \mbox{ , } t \in [0,1].](http://upload.wikimedia.org/math/3/8/7/3870839539dcde1329de7b07b09bfff2.png)

![\mathbf{S}:[t_0, t_{m-1}] \to \mathbb{R}^2](http://upload.wikimedia.org/math/9/2/c/92ccdb3508680f30d3a1c2bcbda02db4.png)
![\mathbf{S}(t)= \sum_{i=0}^{m-n-2} \mathbf{P}_{i} b_{i,n}(t) \mbox{ , } t \in [t_{n-1},t_{m-n}]](http://upload.wikimedia.org/math/e/d/5/ed56946ccf2a0463661b36606cecb760.png) .
.







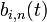




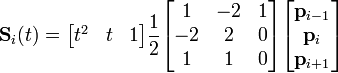 para
para ![t \in [0,1], i = 1,2 \ldots m-1](http://upload.wikimedia.org/math/c/5/2/c525eb4e77ed286a7e4145114dc40cc2.png)
![\mathbf{S}_{i} (t) = \sum_{k=0}^3 \mathbf{P}_{i-3+k} b_{i-3+k,3} (t) \mbox{ ; }\ t \in [0,1]](http://upload.wikimedia.org/math/7/2/d/72d8015a44dab45cfb32197078b0813f.png)

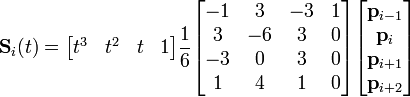 para
para ![t \in [0,1].](http://upload.wikimedia.org/math/d/e/4/de4ef1e33d30a0fa6fc661f8fed20bde.png)

No hay comentarios:
Publicar un comentario